Sine Wave Animated Motion

Animated Motion of a Torus using the Sine Wave Function

Sine wave motion can be used to define animation path, like the GIF animation on the right with the torus moving up and down.

Sine Wave Function

sin( x ) = y

Sine Wave Function sin(x) = y

The Sine Wave is a mathematical formula that describes the behavior of an oscillation pattern. Visually, it looks like a curved line that goes up and down periodically. When the oscillating curve goes up is mathematically predictable and influenced by the x component in the sine wave function.

As the curve travels across the X axis, the curve will go up and down along Y axis. You’ll find it the torus motion from the video tutorial to be very similar to this sine wave curve graph; the torus goes up and down, stamping footprints all over the grid. You can think of the X axis in the graph represented as the timeline in Houdini.

As the animation plays forward, the value of the current frame number, which is $FF increases. What happens to the height of the torus? It moves up and down! Just like the sine wave in the graph. But you might be wondering how is the torus moving forward as well as up and down?

Torus Animation Motion (Sine Wave Motion HScript)

In the Translate parameters of the torus node drive its animation motion. In the Y parameter of the Translate contains the following Houdini expression:

-4.5*(abs(sin($FF*5)))

Let’s take this apart for analysis. This is a basic sine wave function with a bit of variation added to the formula to tweak the motion. The basis of the function is still a sine wave that uses $FF to drive the sine wave.

If you recall the above sine wave graph and sine wave function:

sin( x ) = y

The input of the sine wave is the X axis of the graph, which can be represented by the sequential frame counting forward in the timeline as the animation plays forward. Therefore

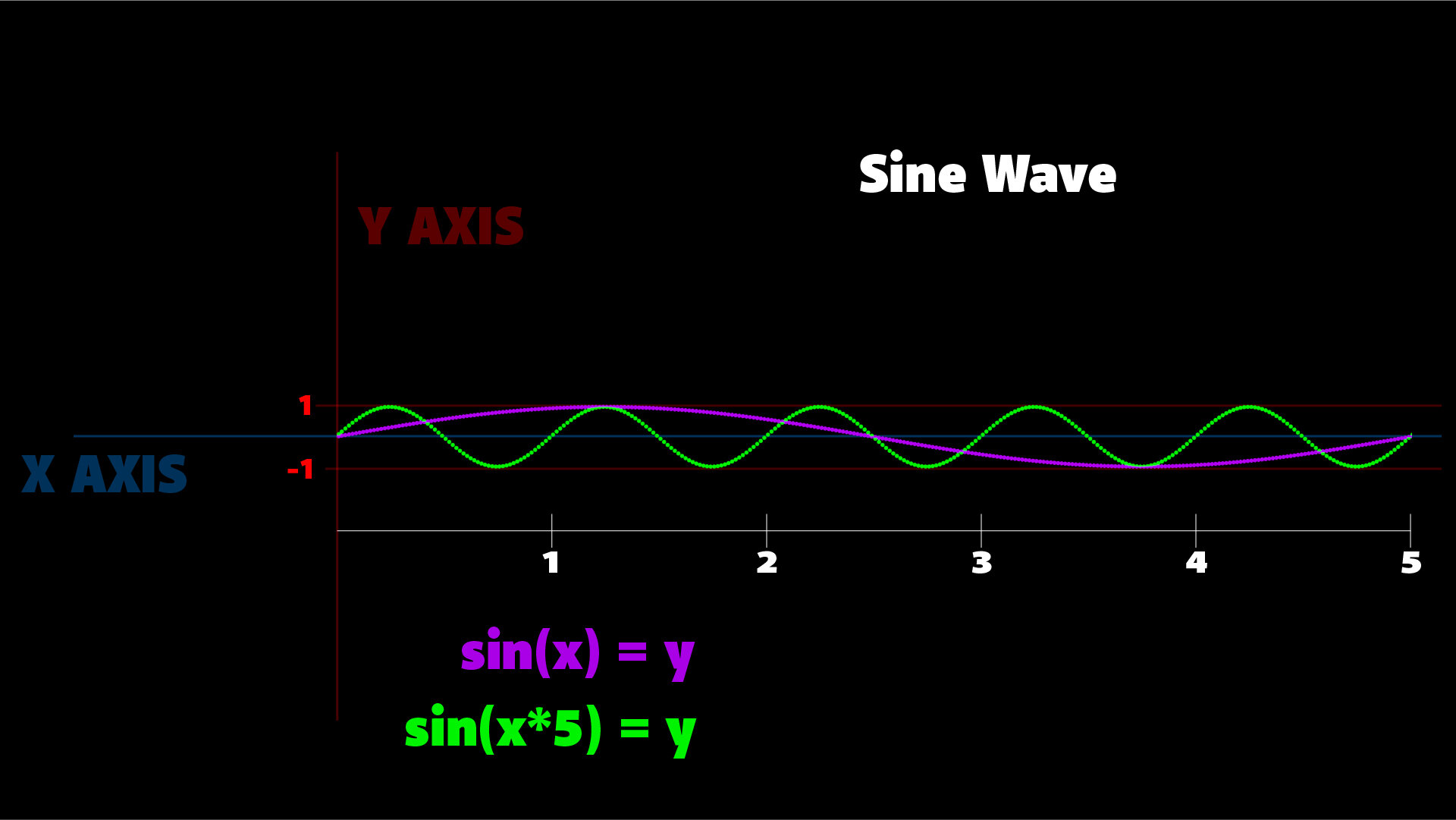
sin($FF)

Comparison between a sine wave with 5 times the frequency and a normal sine wave.

where $FF is a Houdini expression that grabs the current frame number in the scene. 5 is then multiplied to the $FF and then used as the input of the sine function.

sin($FF*5)

This changes the sine function by increasing the frequency of the curve; this means that the curve goes up and down more often in a shorter time frame. As the same number of frames plays in the animation, the torus will move more with greater frequency. In the diagram on the right, the green curved line goes up and down 5 times exactly the same time as the purple curved line goes up and down once.

abs(sin($FF*5))

Absolute value of the Sine Wave.

abs() is the Houdini expression function that takes the absolute value of the resulting curved sine wave. By applying abs(), the function ONLY returns positive values.

Multiplying a number to the sine wave results in greater amplitude, stretching it up higher.

(Sorry the previous image in this spot was displaying the wrong sine formula, I have corrected this now.)

4.5*abs(sin($FF*5))

We then multiply 4.5 to the existing sine function, which will result in the sine wave being stretch up. It will have higher amplitude. The curved line will go up higher.

-4.5*abs(sin($FF*5))

Negative Sine Wave will flip the curve on the X Axis

Multiplying a negative to the sine wave will result in the whole curved line to be flipped, because all the values are now negative.

Move the Torus Forward (X Component Parameter)

The complicated part is moving the torus up and down, but moving the torus forward doesn’t involve sine wave functions. It simply makes use of the current frame number of the play head and the fact that when the animation plays forward the current frame number increases. Then all we need to do is adjust this number to make it go faster or slower.

2*$FF

This will make the torus move forward twice as fast.

abs(2*$FF)

This applies the abs() function taking the absolute value of the frame number, however our animation is always playing forward and starts at frame 1, so it’s never negative. Therefore applying the absolute value of this isn’t really necessary.

1/10 * abs(2*$FF)

By multiplying the fraction 1/10 to the function, it’ll make it go slower. But we already multiplied 2 to the number to make it go twice as fast, so you might be wondering why would we multiply 1/10 to make it go slower again? Maybe 2*$FF is too fast and adjustments need to be made to make it go slower than 2*$FF.

If we simply the function and reduce the fraction, it becomes:

1/10 * abs(2*$FF)

= 1/10 * (2*$FF)

= 2/10 * $FF

= 1/5 *$FF

So as a result, the torus is moved forward 1/5th of a fraction slower than the timeline play head is playing the animation.