Coordinate Positions are Vectors

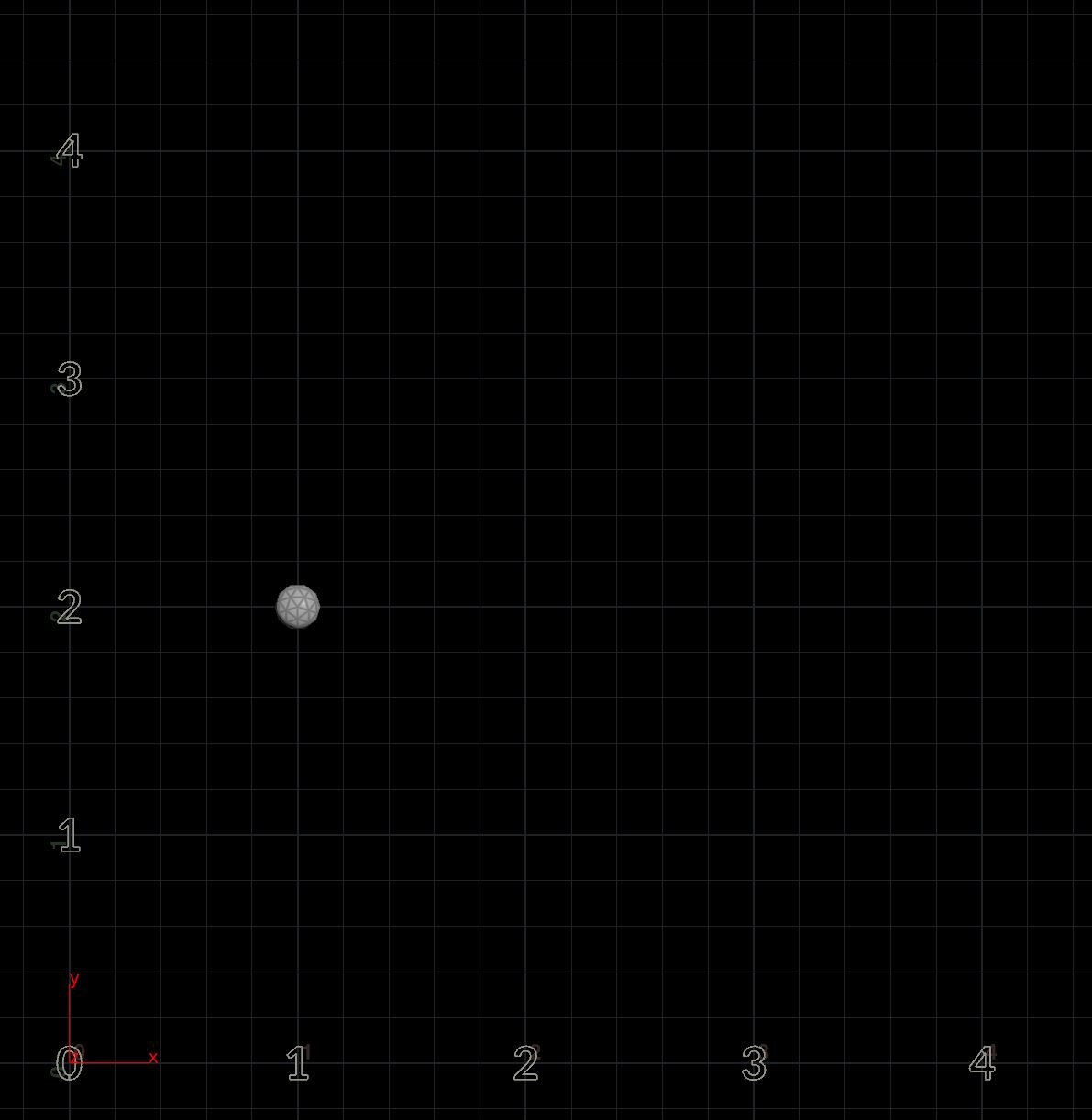
Before getting into 3D coordinates, let’s start with a simple 2D coordinate position (1, 2). This represents a coordinate value of 1 unit to the right on the X axis and 2 units up on the Y axis. This is a position on the 2D grid represented by Cartesian coordinates, which means that numerical units are used to determine the points in a certain space, the grid.

(1, 2) is a unique point in the space of the grid that has a certain distance from the origin. The origin point is (0, 0), the middle of the grid. (1, 2) position is 1 unit on the X axis away from the origin point and 2 units on the Y axis that is away from the origin point. Therefore every unique coordinate has two points associated with it. They will always have a common origin point, which is (0, 0).

Vectors

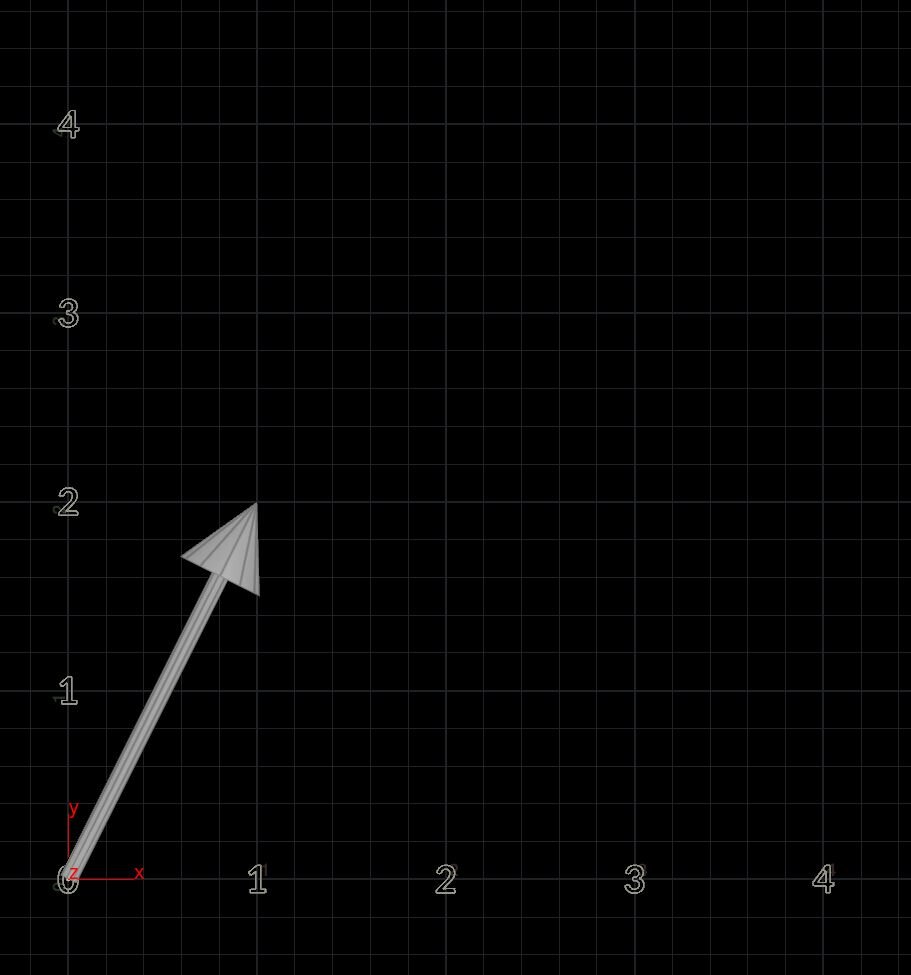
Given two points, we can form a vector. Vectors have direction and magnitude. Since there are two points, we have direction. You start at the origin point and head toward the (1, 2) coordinate, this will determine the direction.

Every Point is Actually a Vector

This is the same for position values in 3D space, but 3D space has an additional axis, the Z axis. Let’s take the coordinate position value of (1, 2, 5). This is a vector, because we know that is has a common origin point, (0, 0, 0). We can draw a line from the origin to the P position (1, 2, 5).

In Houdini, geometry is made up of points and each point has a coordinate position value.

Points on a Sphere

Let’s take a sphere as an example, it’s a polygon made up of points and primitive surfaces. If we ignore all the primitive surfaces for now and focus only on the points that make up there sphere, we will realize that each point on the sphere are actually vectors. Every 3D point in Houdini has a coordinate in 3D space and is a unique vector.

In order to illustrate this, please see the screenshot on the right, where vector arrows are drawn on one side of the surface of the sphere. There should be vector arrows pointing all over the sphere, but there are too many points to view. For simplicity, I am only illustrating a certain area of the vectors P’s of the sphere.

This is all the arrows pointing towards the sphere in with the sphere in wireframe display.

Here’s another shot of the vector points on the sphere, but this time I colored the sphere for clarity.

Vectors Come in Handy

Now that we know all points have what it takes to be vectors, this is very useful. Vectors can be manipulated with addition and subtraction resulting in new directional and magnitude values. In one of my tutorial videos I use vector subtraction to calculate the distance between two points in order to assign color values to the geometry. Normals are all vectors with direction that come in handy for all sorts of tasks like bulging effects. Edge forces in Houdini can be used to define the direction on points on a line.